The math of networks: Random walks and Google PageRank
(0)Random walks on networks, explored by simulation and calculations, with connection to Google PageRank
Prerequisite Knowledge
- Know how to calculate probabilities based on equiprobable events.
Learning Objectives
- Recognize how a collection of nodes and edges can be used to define a random walk.
- Estimate a long-run distribution via simple simulation using a die.
- Calculate location probabilities for random movements on a network.
- Recognize the use of a random walk on a graph in applications, such as in Google PageRank.
- Appreciate when a random walk on a graph will have a long-run distribution.
Description
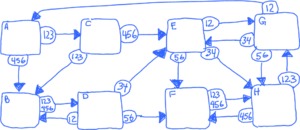
This activity will take about 60 minutes. It focuses on random walks on networks, and connections with Google's PageRank algorithm. The network consists of vertices and paths (directed edges) between them. At each step of the random walk, you choose with equal probability one of the paths that leaves the current vertex. The long-term probabilities of this random walk, which can be thought of as "the percentage of visits to each vertex", correspond to the "PageRank" used by Google to rank web search results.
Students will learn about random walks on networks and explore their behavior via i) simulation with dice and ii) drawing tree diagrams. Connections with PageRank are made. They are then asked to consider networks with structure that is problematic for PageRank (eg absorbing state) and identify those problems.
Suggested Uses, Tips and Discoveries
An "instructor notes" resource describes how this resource might be presented, including materials needed.
Creator
- Chipman, Hugh
Resource Type
Related Resource
The game of Monopoly provides another example of a random walk on a graph. See I. Stewart, "Monopoly revisited", Scientific American, vol. 275, pp. 116-119, 1996
Date Created
Date Approved
Access
Everyone
optional - R code used to compute pagerank (1 of 2)
optional - R code used to compute pagerank (2 of 2)
https://statspace.elearning.ubc.ca/handle/123456789/330

Comments
Ratings in detail